
מכירים את הסיפור על איש בעל חזון שפוטר מחברה רק כדי לחזור אליה כעבור כמה שנים כמנצח עם טכנולוגיה חדשנית? לא, אנחנו לא מתכוונים לסטיב ג'ובס, אלא לג'ון לאסיטר - אנימטור שפוטר בשנות השמונים מאולפני וולט דיסני בגלל התלהבותו מאנימציה ממוחשבת. בהמשך הוא הקים את מה שמוכר כיום כחברת "פיקסאר", חברה ששינתה את עולם האנימציה וזכתה עד כה ב-17 פרסי אוסקר. רגע, אבל מה הקשר למתמטיקה? וכיצד מסייעות פונקציות מסוימות לשפר את תזוזת הדמויות באנימציה ואת האמינות שלהן?
פרסומת
אם נצפה בסרטי אנימציה ישנים או בתוכניות ילדים בסיסיות, נשים לב לדמויות אנימציה אשר מתניידות באופן בלתי משכנע בעליל או לבעייתיות בשיקוף רגשות בתווי הפנים של הדמויות. ראו להלן סרטון להמחשה.
אז איך נוכל להזיז דמויות בצורה משכנעת? בעזרת מתמטיקה כמובן.
נפתח בשלושה מושגים אשר דרושים לנו בהמשך: קוֹאוֹרְדִּינָטוֹת, קואורדינטות בָּרִיצֶנְטְרִיוֹת וקואורדינטות הערך הממוצע. קואורדינטות הן סדרות מספרים המציינת את מיקומו של גוף במישור או במרחב. המוכרות ביותר הן קואורדינטות קרטזיות המתייחסות למערכת צירים דו-ממדית עם ציר X וציר Y המאונכים זה לזה. בגאוגרפיה נעזרים בהן לציון קווי אורך ורוחב. קואורדינטות בָּרִיצֶנְטְרִיוֹת (Barycentric Coordinates) הן מערכת קואורדינטות שבה מתואר מקומה של נקודה ביחס לקודקודי משולש. נקרא למשולש הזה כלוב. כל נקודה בתוך הכלוב מיוצגת על-ידי שלושה פרמטרים, בדרך כלל (α, β, γ), כאשר הערכים α, β ו-γ מתקבלים כתלות במרחק בין הנקודה לקודקודי הכלוב [1]. קואורדינטות בריצנטריות נמצאות בשימוש נפוץ ביישומים מגוונים כגון: גרפיקה ממוחשבת, אנימציה, סימולציות פיזיקליות, התנהגות של חומרים, שיטות אלמנטים סופיים ועוד. אופן הזזת הדמות מתבצע על-ידי הזזת קודקודי המשולש ואז כל נקודה של הדמות זזה בהתאם לשינוי הקואורדינטות שלה [2]. החיסרון הברור של קואורדינטות בריצנטריות הוא שהן תומכות בכלוב משולש בלבד וזה מגביל מאוד את האפשרויות להזיז את הדמות. אם אנחנו רוצים לשלוט בדמויות אנימציה מורכבות, צריך כלוב מורכב יותר. קואורדינטות הערך הממוצע הן הכללה של הקואורדינטות הבריצנטריות אשר תומכת גם בכלוב בעל קודקודים רבים יותר, כלומר מצולע. נדגיש שהגדרת קואורדינטות הערך הממוצע מתבססת על הבריצנטריות: מחלקים את הצורה למשולשים רבים מאוד, ואז משתמשים בקואורדינטות בריצנטריות של המשולשים.
הנה כמה דוגמאות להמחשה. דוגמה להזזת דמות בקואורדינטות בריצנטריות:
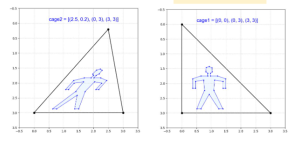
דוגמה לאופן השימוש בכלוב מצולע בקואורדינטות הערך הממוצע:

עכשיו כשהמונחים מובנים, אפשר להתחיל. באנימציה אנחנו מצפים שתנועת עצמים על המסך תהיה דומה לתנועה בעולם הממשי. לכן האתגר של האנימטורים הוא לדאוג שהתנועה תיראה טבעית והאנימציה תהיה נעימה לעין [3]. דמות במישור או במרחב מיוצגת על ידי מספר רב מאוד של נקודות, בדרך כלל אלפים ויותר. על מנת להזיז את הדמות יש להזיז כל נקודה ונקודה באופן המתאים בכדי להשיג אפקט של תנועה טבעית שאינה מעוותת את הדמות. זוהי כמובן משימה חישובית מייגעת ומורכבת מאוד. על מנת לקצר זמנים ולחסוך בכוח חישוב, משתמשים בשיטות שונות. אחת מהן היא חסימת הדמות בתוך כלוב אשר מורכב מרשת קטנה של קודקודים, בדרך כלל עשרות עד מאות בודדות. כל נקודה על הדמות תקבל סדרת קואורדינטות המתארות את המיקום היחסי שלה ביחס לקודקודי הכלוב. לאחר כל שינוי של הכלוב יש לחשב מחדש את כל קודקודי הדמות על ידי שימוש בקואורדינטות הללו ביחס לקודקודי הכלוב החדש (Image cloning). הרעיון הוא שבמקום להזיז את כל הנקודות המרכיבות את האובייקט, פשוט מזיזים את קודקודי הכלוב ואז כל נקודה על הדמות זזה בהתאם לשינוי הקואורדינטות שלה המחושבות ביחס למיקום החדש של קודקודי הכלוב. דמיינו שאתם צריכים להזיז 100 חלקי לגו. להזיז אותם בתוך קופסה קל בהרבה מאשר להזיז אותם אחד אחד. מכירים את התמונות המצחיקות של שחקנים הלבושים בבגד גוף עם חיישנים? זו דרך לשלוט על הכלוב בצורה מיטבית. החיישנים משדרים בצורה שוטפת את הקואורדינטות שלהם וכך מאפשרים ליצור אנימציה חלקה ואמינה. הבעייתיות בקואורדינטות הערך הממוצע היא שבמצבים מסוימים נוצרים עיוותים וזיופים.
נביט לדוגמה בחתול שראינו קודם:

בתמונות רואים בבירור עיוות של הרגל האחורית. לכן נעשו מאמצי מחקר נוספים למציאת מערכות קואורדינטות טובות יותר. אחד מהפיתוחים של פיקסאר מתבסס על פונקציות הרמוניות [4]. במובנים רבים פונקציות הרמוניות מתארות ומבטאות תהליכים פיזיקליים וכן תופעות אשר נראות לנו טבעיות. פונקציה הרמונית מתאפיינת ב״עקרון הממוצע״, לפיו הערך של כל נקודה שווה לממוצע הערכים של הפונקציה בעיגול סביב הנקודה. ניקח לדוגמה שדה חיטה מוקף בגדר ונניח שיש פונקציה הרמונית אשר מתארת את הגובה של כל גבעול. המשמעות של עקרון הממוצע היא שלא משנה באיזו נקודה נעמוד, הגובה הממוצע של הגבעולים על פני שטח עגול מסביב תמיד יהיה שווה לגובה הגבעול במקום שבו אנחנו עומדים.
הרעיון בקואורדינטות הרמוניות דומה לקואורדינטות הערך הממוצע והוא הולך בערך כך: חוסמים את הדמות בכלוב, לכל קודקוד בכלוב מתאימים פונקציה הרמונית מתאימה ואז כל נקודה על הדמות מקבלת קואורדינטות ביחס לפונקציות ההרמוניות של הכלוב. הזזת הדמות עובדת באופן דומה על ידי הזזת קודקודי הכלוב וחישוב השינוי בקואורדינטות. התכונות המיוחדות של פונקציות הרמוניות ״מתקנות״ את הבעיות שהיו לנו בקואורדינטות הקודמות. כדי להבין את ההתאמה לעומק כדאי להתרשם מדוגמה [7], ולצפות בסרטונים בסעיף 3.3 של החתול ההרמוני. מעניין לציין שהפונקציות ההרמוניות הללו אינן ניתנות לתיאור ״יפה״ כמו הפונקציות שרובנו מכירים. למעשה קשה מאוד לחשב אותן במדויק. עם זאת, בעזרת שיטות של חישובים מקורבים, ניתן לבטא את הפונקציות בצורה ״קרובה מספיק״. כפי שאפשר להניח בהיגיון בריא, ככל שהקירוב יהיה טוב יותר, התנועה תיראה לנו טבעית יותר.
לקינוח נחזור לסיפור של ג'ון לאסיטר ופיקסאר. ההתלהבות של לאסיטר מטכנולוגיית האנימציה הממוחשבת התנגשה עם רצון הבוסים שלו, והוא פוטר ב-1983. לאחר מכן הוא החל לעבוד בחטיבת הגרפיקה הממוחשבת של לוקאספילם (Lucasfilm Ltd), ושם ביים סרט אנימציה קצר, אחד הראשונים שהציגו דמויות ממוחשבות - The Adventures of André and Wally B. בשנת 1986 החטיבה נרכשה על ידי Apple Computer Inc ונהפכה לחברה עצמאית בשם פיקסאר. סרטם "צעצוע של סיפור" מ-1995 היה הסרט הראשון באורך מלא שנעשה באנימציה ממוחשבת ובהדמיה תלת ממדית. ב-1 בנובמבר 2011 קיבל לאסיטר כוכב בשדרת הכוכבים של הוליווד [5]. אז מלבד הרכילות המעניינת, חברת פיקסאר פיתחה טכנולוגיות רבות לאנימציה ממוחשבת וקידמה את התחום. לדוגמה, אחד הפיתוחים הידועים שלהם הוא טכנולוגיית אנימציה בשם Surface subdivision שכתבנו עליו בעבר. הטכנולוגיה הופכת מצולעים שנשמרו במחשב לצורות עגלגלות, שנראות עדינות, נעימות ואנושיות יותר [6]. זו דוגמה מעולה לשילוב בין אמנות למדע, שממחישה כיצד שני התחומים תורמים זה לזה.
עריכה: שיר רוזנבלום-מן
מקורות לקריאה נוספת:
- קואורדינטות בָּרִיצֶנְטְרִיוֹת
- אלמנטים סופיים
- להזיז צורה על המסך
- פונקציות הרמוניות
- על ג'ון לאסיטר
- לעגל ולעדן את המלבן
- שימושים של פונקציות הרמוניות באנימציה ממוחשבת










