About 2300 years ago the Greek Mathematician Eratosthenes conducted a simple and ingenious experiment: He measured the Earth's radius with astonishing accuracy using two sticks. How did he do it?
Advertisement
We all know that Earth is round—except for the Flat Earthers— but how can we measure its radius? The planet’s circumference can be determined directly by ship voyages, as was done hundreds of years ago. Once the circumference is known, the radius can be calculated precisely. The radius of Earth is approximately 6,370 km. It is not exactly uniform because Earth is not a perfect sphere. Yet to a good approximation it is, in fact, smoother than a regulation billiard ball [2]. So how was it possible to measure the radius 2,300 years ago?
Eratosthenes had a brilliant idea. Suppose we have two identical sticks placed far apart on the Earth’s surface. If the Earth is spherical, sunlight will cause the sticks to cast shadows of different lengths at exactly the same time. Take a look at the illustration depicting this concept.
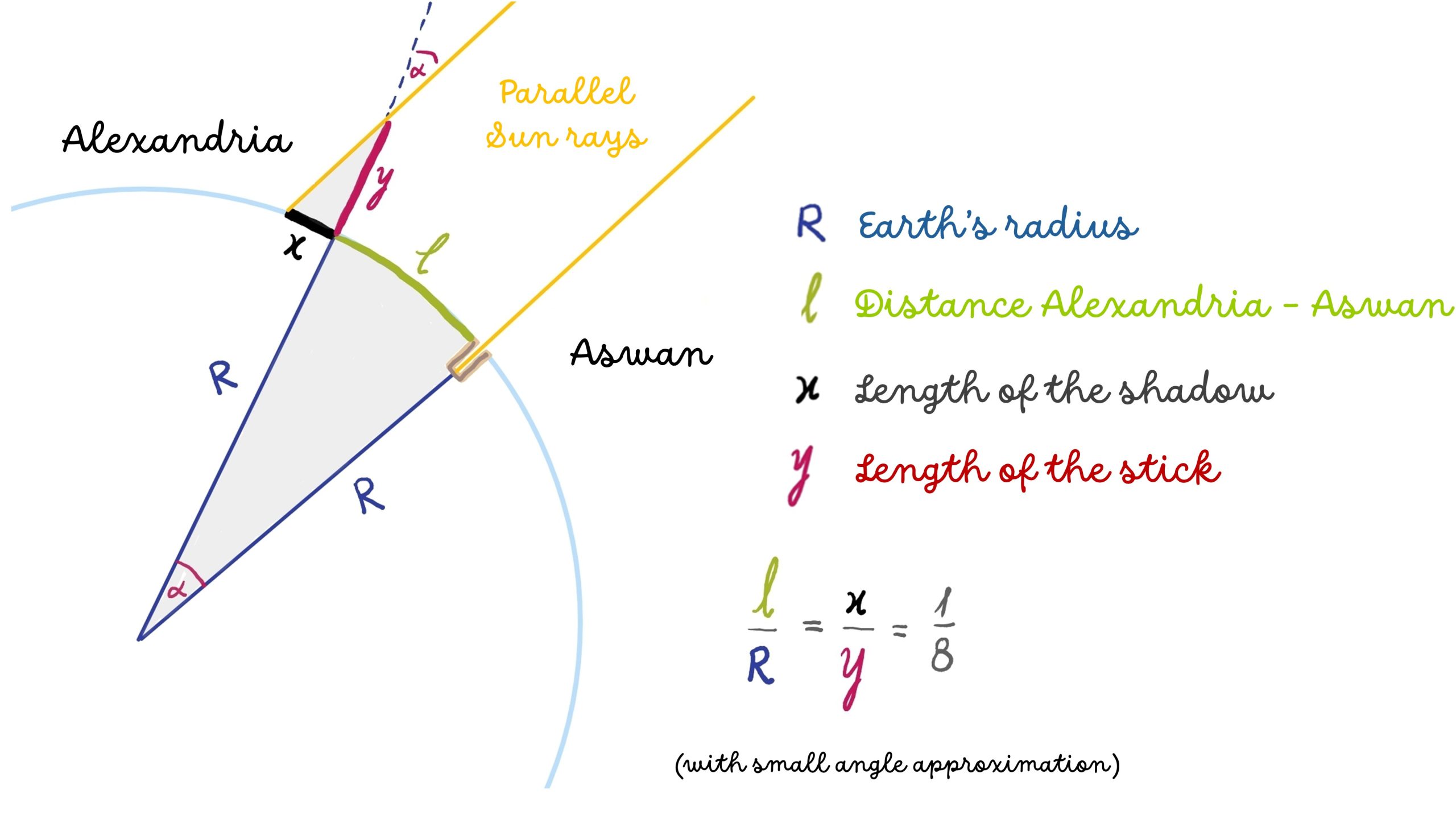
Illustration: Noa Zilberman | Translation: Gloria Volohonsky
Now, let’s review the experiment in detail. On June 21, the longest day of the year, Eratosthenes was in Aswan, Egypt. He waited until noon, when the Sun was directly overhead at its Zentih. How did he know the Sun was exactly overhead? There was a well in Aswan whose bottom was illuminated by sunlight without the rays touching its sides at the moment of zenith. This meant that if a stick were placed perpendicular to the ground in Aswan at noon on June 21, it would not cast a shadow.
Eratosthenes sent a man to Alexandria, about 800 kilometers away, to measure on the length of the shadow cast by a stick when the Sun was at its peak on the same day and to record the length of the stick as well. The ratio of the stick's length to its shadow was found to be approximately 8:1. Using simple geometry, as shown in the diagram, it is possible to demonstrate that the Earth’s radius is approximately equal to the distance between Aswan and Alexandria multiplied by the ration of the stick's length to its shadow. That is, 800 km multiplied by 8 equals 6,400 km. Not a bad achievement for a calculation performed 2,300 years ago!
This calculation relies on the assumption that the Sun is very far from Earth. Eratosthenes did not know, as we do today, that the distance between Earth and the Sun is approximately 150 million kilometers. However, the assumption that the Sun is extremely distant was reasonable in his time.
Suppose for a moment that the Sun is at a close distance to us and that Earth is flat. According to the geometry shown in the next illustration, the Sun would be hanging 6,400 kilometers above us. However, this is implausible for many reasons. For starters, if the Sun were that close to Earth, we would all be scorched by its heat.
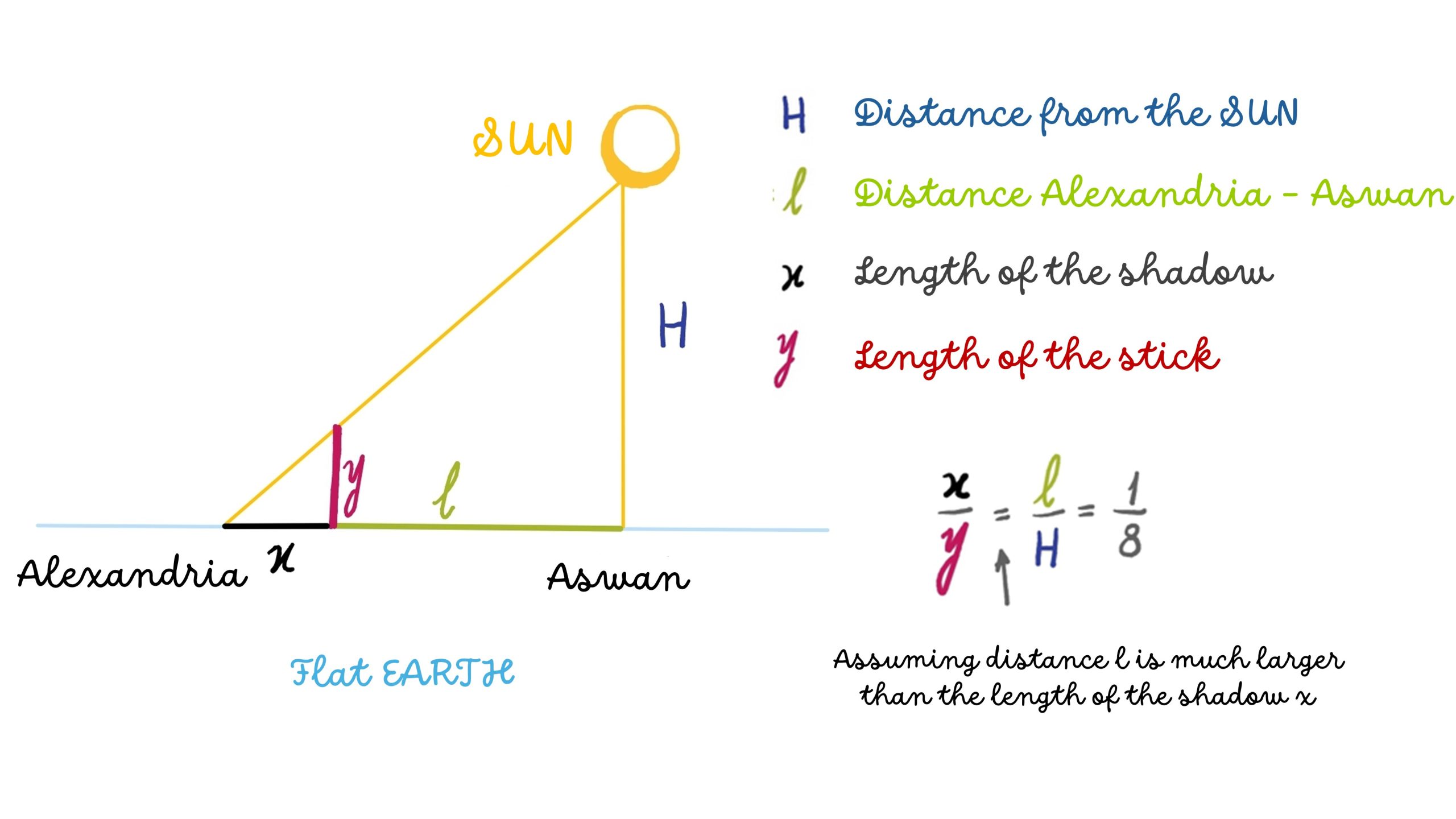
Illustration: Noa Zilberman | Translation: Gloria Volohonsky
Rest assured, we now know that the Earth is indeed spherical, and its radius was calculated nearly 2,300 years ago.
Hebrew editing: Smadar Raban
English editing: Gloria Volohonsky
References:
Adi is a professor of theoretical particle physics at Swansea University. His research focuses on quantum chromodynamics and string theory.
Noa holds a PhD in Physics from the Technion and is currently a postdoctoral researcher at the Princeton Gravity Initiative at Princeton University. Her research focuses on quantum effects on black hole backgrounds. She also serves as a scientific editor at “Little, Big Science".
