The distance between the Sun and the Earth is about 150 million kilometers. How do we know this? How was this distance estimated over 2000 years ago?

The Sun, which appears to us as a yellowish ball of fire, is an enormous celestial body that supplies the energy required for life on Earth. The Sun’s mass is immense compared with Earth’s, and therefore we orbit the Sun slowly—a revolution that lasts a year. But how do we know the distance between us and the Sun? It turns out that people in ancient Greece already knew that the Sun is very far away from us, and the early astronomers even tried to estimate that distance.

The story begins with Eratosthenes measuring Earth’s radius, which we described in a previous post [1]. With a stick, some simple mathematics, and above all a brilliant idea, Eratosthenes estimated Earth’s radius to be 6,400 km—already 2,300 years ago! Amazing, isn’t it?

The second chapter of the story is the measurement of the distance between Earth and the Moon, carried out for the first time by Aristarchus of Samos. Once Earth’s radius is known, we can estimate the distance between us and the Moon. How? The trick is to use a lunar eclipse. During a lunar eclipse, Earth casts a large shadow in space and the Moon passes through it (see illustration).

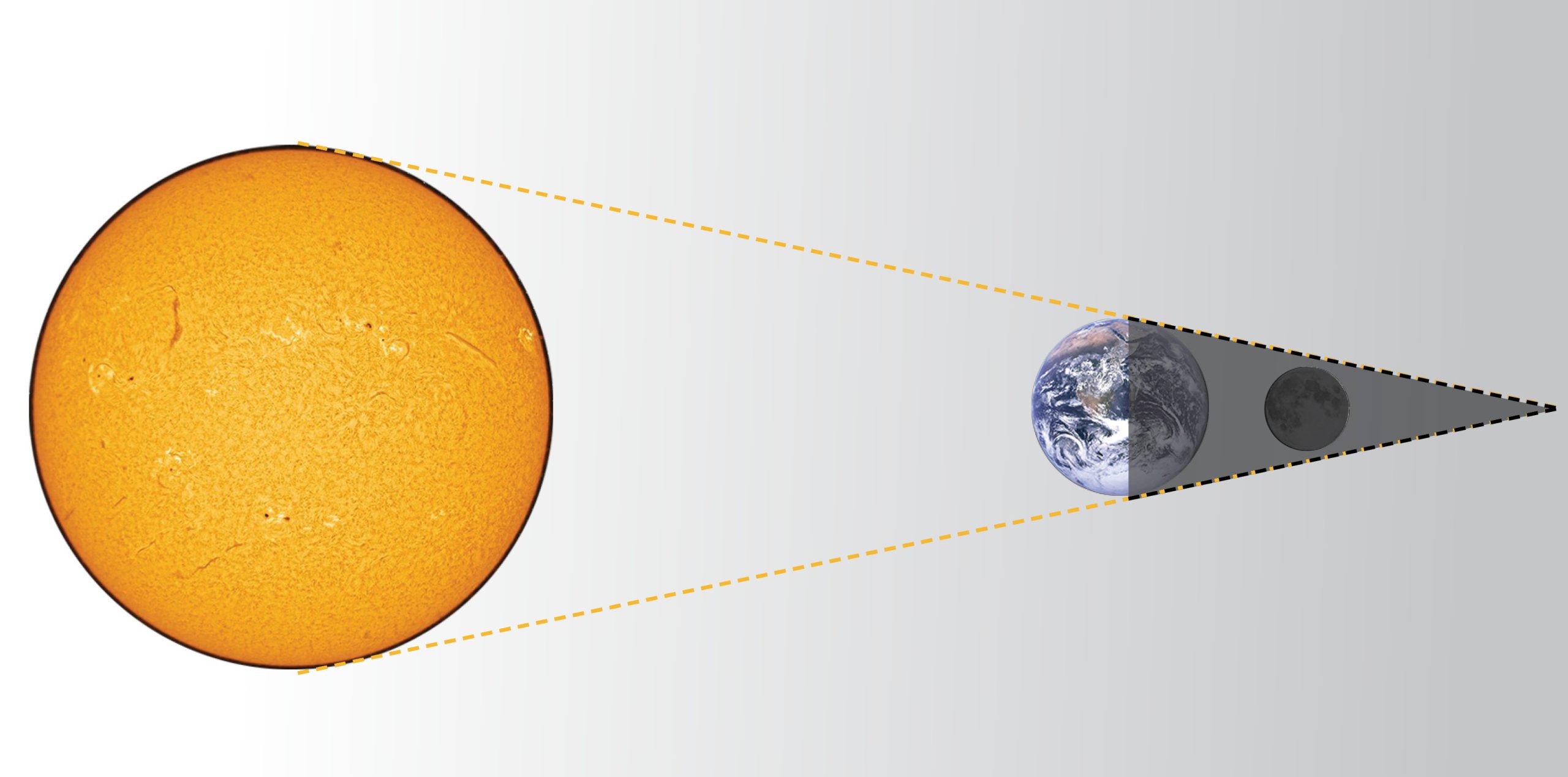
For about four hours the Moon is not visible because it is inside the shadow, whose size equals Earth’s diameter. This darkness is useful, since the ratio between the length of the shadow—namely Earth’s diameter—and the circumference of the Moon’s orbit around Earth equals the ratio between the duration of the eclipse and the duration of the orbit (a lunar month—28 days):

4 hours / month = Earth’s diameter / circumference of the Moon’s orbit

From this equation one can extract the circumference of the circle in which the Moon orbits Earth. Because the circumference of a circle equals the radius multiplied by 2π, we can determine the circle’s radius, i.e., the distance from Earth’s center to the Moon’s center. In this way the Greek scholar Aristarchus concluded that the distance between us and the Moon is about sixty times Earth’s radius. This is an excellent estimate. Have we mentioned that Aristarchus was a genius?

And now, with this information in hand, Aristarchus used the following elegant idea to estimate the distance between us and the Sun: Imagine the moment in the month when we see a half Moon, roughly a quarter of the way through the month. The reason we see only half the Moon is that one half is illuminated by the Sun, while the other half is in Earth’s shadow (see illustration).

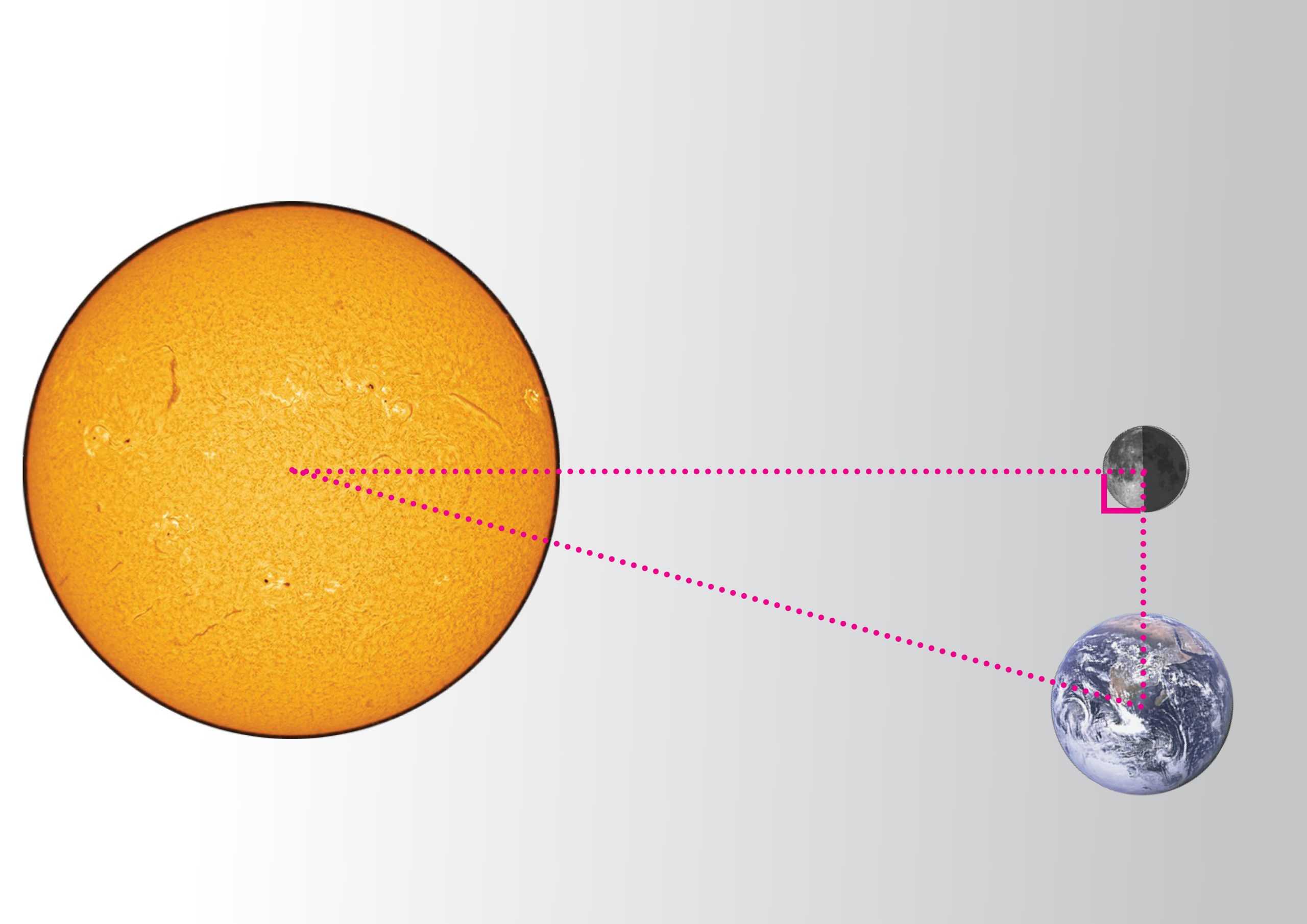
The crucial point here is that the three celestial bodies—Earth, the Moon, and the Sun—form a right-angled triangle (turns out geometry lessons matter) with a very small apex angle. The short leg of the triangle is the distance between Earth and the Moon, while the hypotenuse is the distance to the Sun. The small angle, or its complement, can be estimated by observing the Moon and the Sun, because Earth is located at the vertex of the complementary angle (see illustration). However, Aristarchus greatly erred in estimating the size of that angle, and therefore he concluded that the Sun’s distance from Earth is about twenty times the distance between Earth and the Moon, whereas in fact the Sun is about 390 times farther away. Even so, this was an impressive achievement for simple science without telescopes or clocks.

Since the Sun and the Moon appear from Earth to be roughly the same size but the Sun is much farther away, Aristarchus inferred that the Sun is much larger than both the Moon and Earth. Therefore, he argued, it is reasonable that Earth orbits the Sun, not the other way around as was believed at the time. In this Aristarchus preceded Copernicus by about 1,700 years!

Measurement techniques improved dramatically with the advent of new, more precise technologies such as parallax measurement. Parallax is the phenomenon in which an object’s apparent position changes relative to the background. For a simple demonstration, place a finger in front of your face, close one eye, and then close the other: the finger will appear to shift against the background. Similarly, one can observe a planet like Venus from two locations separated by a known distance. Given the baseline between the observation points, measuring Venus’s shift against the celestial background allows us to calculate quite accurately the planet’s distance from Earth. Using models of the solar system, we can then calculate the distance to the Sun with high precision.

Edmond Halley (after whom the famous comet is named) devised a calculation method based on transits of Venus across the Sun. When a particular transit is observed from different places on Earth, Venus’s path appears different against the Sun—another application of parallax that enables precise measurement of the distance between us and Venus, from which one can deduce the Earth–Sun distance using Kepler’s laws [2].

Another method relies on radar measurement: by sending a signal to Venus when exactly half of it is illuminated [3] and receiving the reflected signal, one can calculate the distance to Venus, and by the same trigonometric calculation used by Aristarchus, determine precisely the distance to the Sun.

In addition to the methods described here, there is a research probe called the Parker Solar Probe [4], which has approached within 6.5 million kilometers of the Sun! Communication with this probe enables a calculation similar to sending a radar signal to Venus—simply measure the probe’s response time to a signal sent from Earth.

The average distance between Earth and the Sun is called an astronomical unit, and today we know it with high precision: 149,597,870.7 kilometers. This figure is the result of thousands of years of observations, calculations, and improvements in measurement techniques.

Illustration of the angular sizes of various objects (the area they occupy in Earth’s sky)

Hebrew editing: Smadar Raban
English editing: Elee Shimshoni

References:

[1] Measuring Earth’s radius

[2] Kepler’s laws

[3] The phases of Venus

[4] Parker Solar Probe