Advertisement
Spin is one of the most prevalent concepts in elementary particle physics, and also one of the least understood. So what is this mysterious property?
In this article we will explain one of the most fundamental concepts in particle physics—spin. Together with various charges and mass, spin is part of a particle’s “ID card,” a property that describes what different observers must do in order to agree that they are referring to the same particle, and we will soon explain what this means.
We describe particles, elementary or composite, using quantum theory. In quantum theory, a particle is represented by a function that gives, for every point in space, the probability of finding the particle there [1, 2, 3]. Here we encounter a problem whose solution leads to the concept of spin. The problem is that different observers do not necessarily agree on what constitutes a point in space. Our space is described by a coordinate system. There are several operations, called “spatial symmetries,” that we can perform on space without affecting it. In classical physics these operations are:
The first—moving the origin to another point. Because the space is infinite and uniform, a property called homogeneity [4], such a shift does not influence the physics, and two observers who disagree on the location of the origin must still agree on the particles and their behavior.
The second—rotating the coordinate system about any axis. Since space looks identical in every direction, or isotropic as physicists call it [4], it does not change when we rotate it. Again, observers who disagree on the orientation of the axes must still agree on the physics they describe.
The third and last way is to move the origin in some direction with a constant straight-line velocity. Once more, as you have surely guessed, this change does not affect the physical description of the world [5].
The collection of all these operations is called the Galilean group, and it lies at the foundation of classical physics. For the purpose of discussing spin, the first way of changing the coordinate system is irrelevant; only the second and third matter. Before we can explain the concept, we need to understand how the nature of these two operations changes when we leave the framework of Newtonian mechanics and move to Einstein’s theory of relativity. Einstein taught us that there is actually no difference between space and time, and that time should be treated as just another dimension—that is, another axis in our coordinate system. Without going too deeply into technical details, this implies that the third way of changing viewpoint—a constant-velocity shift of the origin—can be described as a rotation of the time axis together with one of the spatial dimensions (as opposed to an ordinary rotation, which rotates two spatial dimensions), though it is a somewhat different kind of rotation from what we are used to. The set of these rotations is called the Lorentz group, and it forms the basis of Einstein’s special theory of relativity. Each of the rotations composing it is called a Lorentz transformation [6].
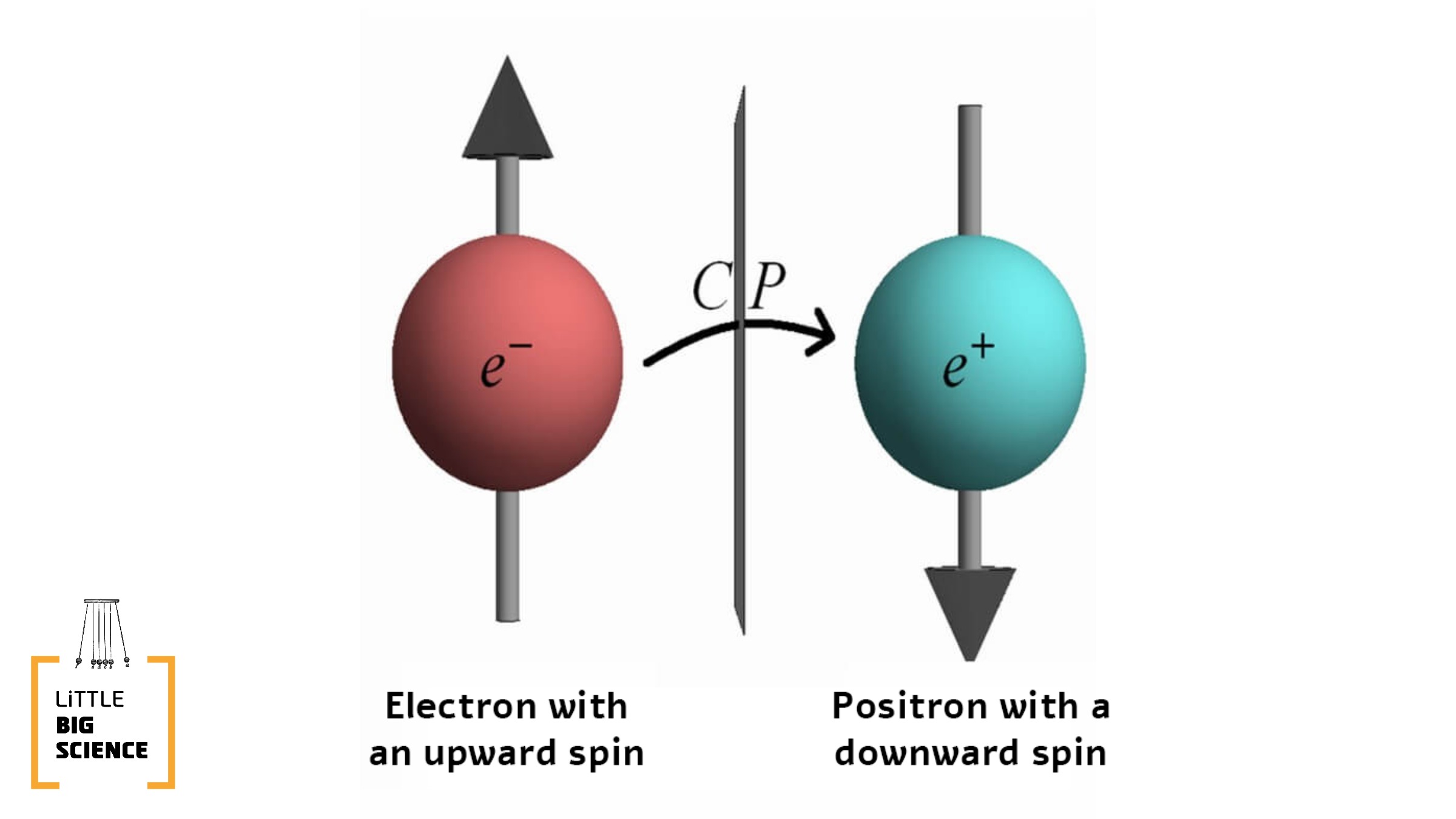
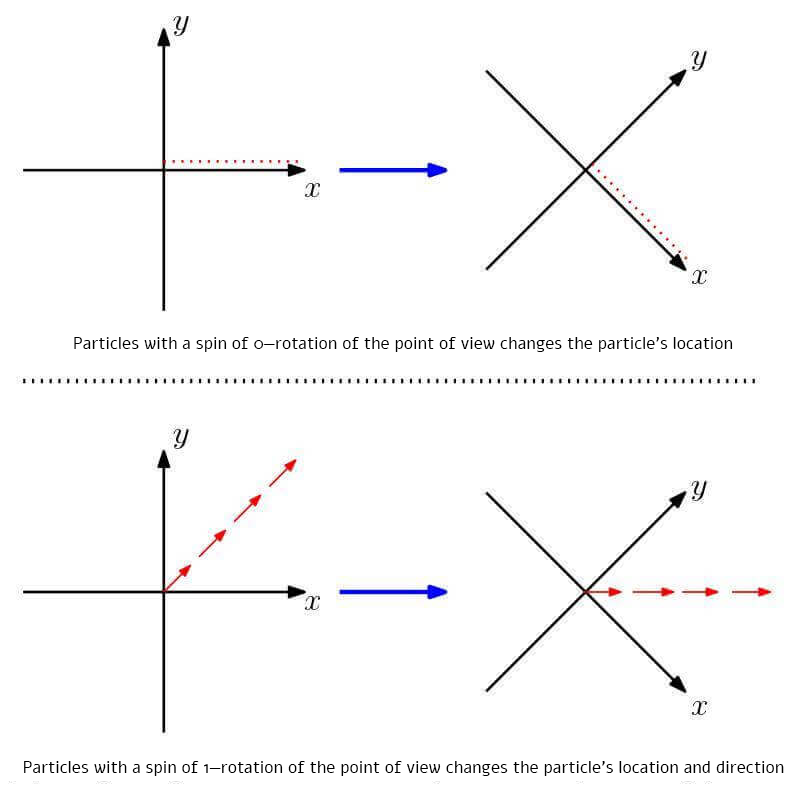
After this long introduction we can finally reach the explanation of spin. Let us imagine two physicists, Bert and Ernie, each of whom describes space using a different coordinate system, but one can transform from one system to the other by a Lorentz transformation. Bert has a function that describes a particle and wants to explain to Ernie how this function will look in Ernie’s coordinate system. Suppose Bert knows that the point he calls A is the point Ernie calls B. He must tell Ernie how his function at point A appears to Ernie at point B. In other words, Bert wants to explain to Ernie what happens to a particle if Bert rotates space (either an ordinary rotation or a Lorentz rotation). The way Bert does this depends on the particle he wishes to describe: for certain particles, such as the Higgs boson, the value of Ernie’s function at point B is exactly equal to the value of Bert’s function at point A. In this case we say the particle has spin zero. For other particles, like the photon, the change is more complicated, and to obtain Ernie's function value at point B we must take Bert’s function value at point A and rotate it in the same manner that we rotate space to get from point A to point B (see illustration). In such a case we say the particle has spin one. More complex ways of calculating the relation between Bert’s and Ernie’s functions give us particles with spin one-half, such as the electron. This is an interesting case because to rotate the electron’s function back to its original state we must rotate it by 720 degrees, or two full turns. Other possibilities can lead to spin two, or any number that is an integer multiple of one-half, all thanks to the Lorentz transformation.
English editing: Elee Shimshoni
References:







