According to the popular notion, a black hole is a sort of bottomless pit that only devours and devours... So you might be surprised to learn that you can gain energy from a black hole—by “feeding” it from a safe spot outside it. This is made possible by the Penrose process: a legal way (under the legal framework of the laws of physics, of course) to “pickpocket” a rotating black hole.
Advertisement
Black holes, which we have written about before[1], are defined by the existence of a one-way boundary known as the event horizon. This invisible point of no return, means that once something crosses it, no signal — not even a ray of light — can escape back into the universe. In the case of a non-spinning black hole (a Schwarzschild black hole), particles that fall in always increase its mass. However, when a black hole is rotating, as real black holes in our universe are, the equations of general relativity add a twist.
The equations of general relativity, also known as Einstein’s equations, describe the relationship between the geometry of spacetime and the matter and energy in the universe. Spacetime bends and warps in response to matter and energy, which in turn move according to this warped geometry. One consequence of this is that a rotating body, for example Earth, “drags” spacetime, forcing it to rotate with it. This phenomenon is known as frame dragging (see Figure 1). Objects located in the dragged spacetime are carried along, like crumbs on a moving tablecloth. For spinning black holes, this effect intensifies to the extreme: close enough to a rotating black hole, there is a region in which it is impossible to resist the drag. Every object, even a photon, is swept up in the whirl of spacetime (see Figure 2). This region surrounds the black hole and lies outside its event horizon, meaning it is accessible and can be escaped. This can be confusing, so let us clarify the difference between the two regions. In the aforementioned strong-dragging region, you can think of spacetime as moving faster than light relative to a distant observer. Therefore, it sweeps up photons, but the motion is around the black hole. Inside the event horizon, you can likewise think of spacetime as moving faster than light and carrying photons with it. However, now the motion is inwards, and therefore this boundary defines the black hole and cannot be escaped.
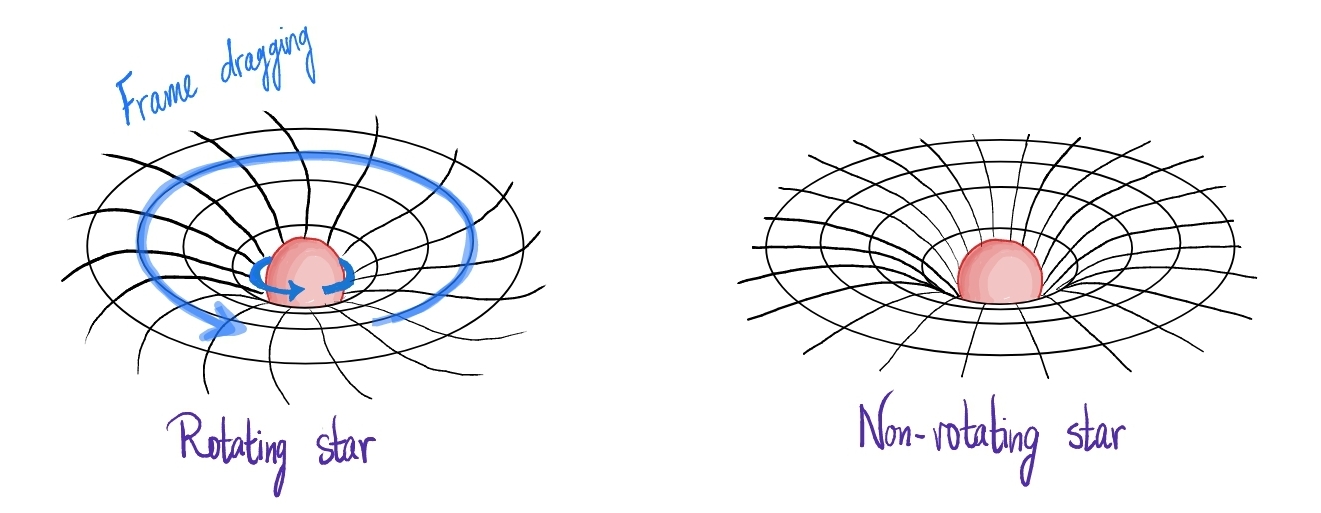
Figure 1: Illustration of the space-time geometry around a non-rotating star (right) and around a rotating star (left). In the case of the rotating star, there is frame dragging, and spacetime acquires a “twist” in the direction of rotation.
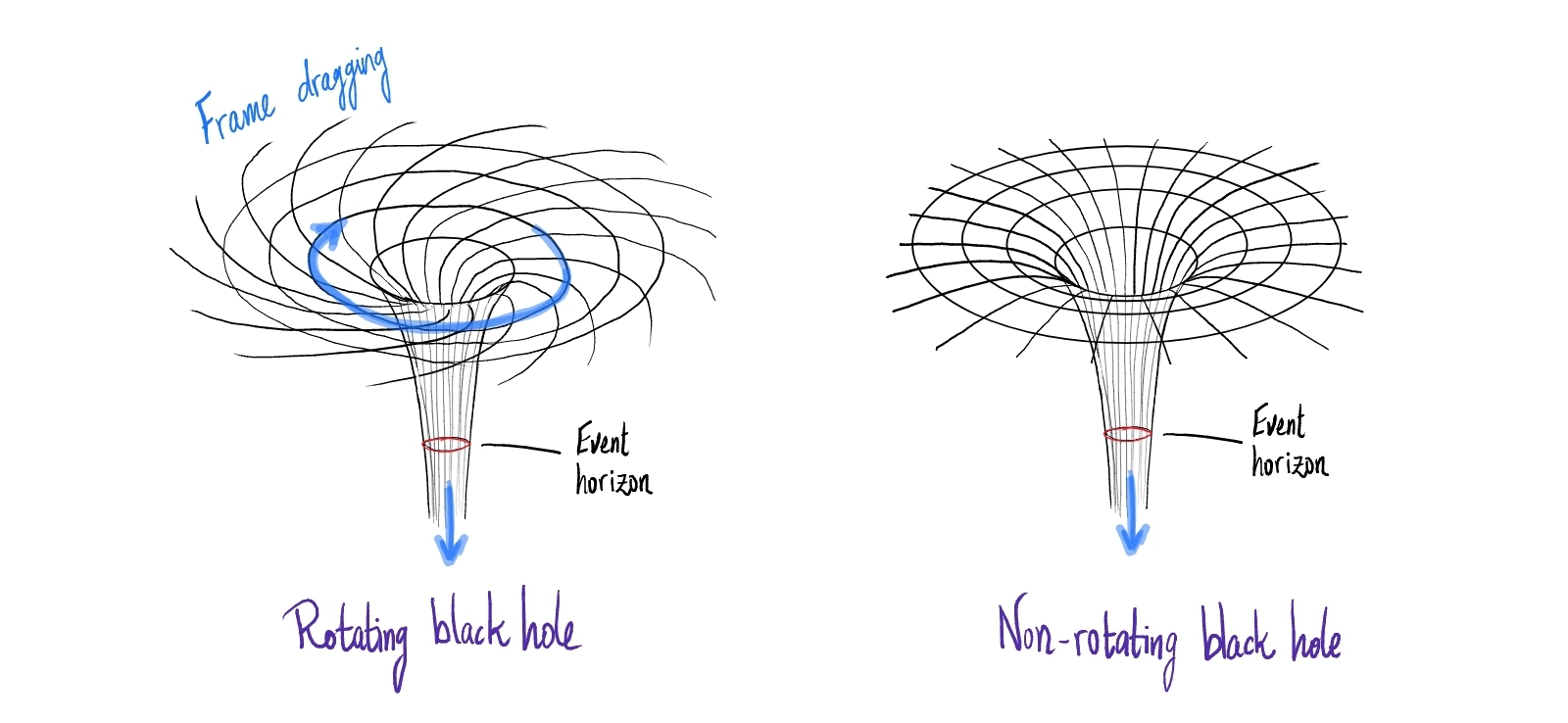
Figure 2: Illustration of the space-time geometry for a non-rotating black hole (right) and for a rotating black hole (left). In both cases, the event horizon is the point of no return, beyond which even light must travel inward. For a rotating black hole there is a strong frame-dragging region in which every object, even light, must orbit the black hole. This region lies outside the event horizon.
Feeling dizzy? So are we. British physicist Roger Penrose, winner of the 2020 Nobel Prize in Physics[2], realized that this swirling drag opens the door to an intriguing thought experiment. His idea gave the region of inevitable swirling its name: the ergosphere. The term comes from the Greek word ergon (work), because in this zone one can, in principle, extract energy from the black hole.
Penrose’s mechanism is entirely classical—there is nothing quantum about it—yet it transfers energy from the black hole to a distant region. Here is how it works [3]: Imagine an astronaut at a safe distance who drops an object (a tennis ball, a printer, an IKEA flat pack, or any other object of your choice) into the ergosphere. Inside, the object breaks into two pieces. This is an ordinary process that conserves energy. The energy of the original object equals the sum of the energies of the two fragments. In a similar process outside the ergosphere, all energies are positive, so each fragment would have less energy than the original object. Here’s the catch: An object inside the ergosphere can have negative energy relative to a distant observer. Suppose one of the fragments produced in the ergosphere has negative energy and crosses the event horizon, falling into the black hole. The other fragment recoils in the opposite direction and is flung back out of the ergosphere with more energy than the original object had, as required by energy conservation (see Figure 3). In short, an object entered the ergosphere with a certain energy, and an object exited with higher energy! In other words, we have stolen energy from the spinning black hole. This additional energy comes from the black hole’s rotational energy. As a result of this process, the black hole slows its spin slightly, and its mass decreases.
Wait, did we reduce the mass of the black hole? Aren't black holes only supposed to grow? Let’s look into this. Indeed, there is a theorem stating that the area of a black hole, as measured by the area of its event horizon, can only increase, as long as quantum effects are neglected. But fear not—it turns out that despite the loss the black hole experiences in this process (in mass and angular momentum), the area of its event horizon still increases as a result of absorbing the object with negative energy. This is related to the fact that the energy is negative only relative to a distant observer. To an observer within the ergosphere, the infalling fragment has positive energy, as it must, and this translates into an increase in the horizon area.
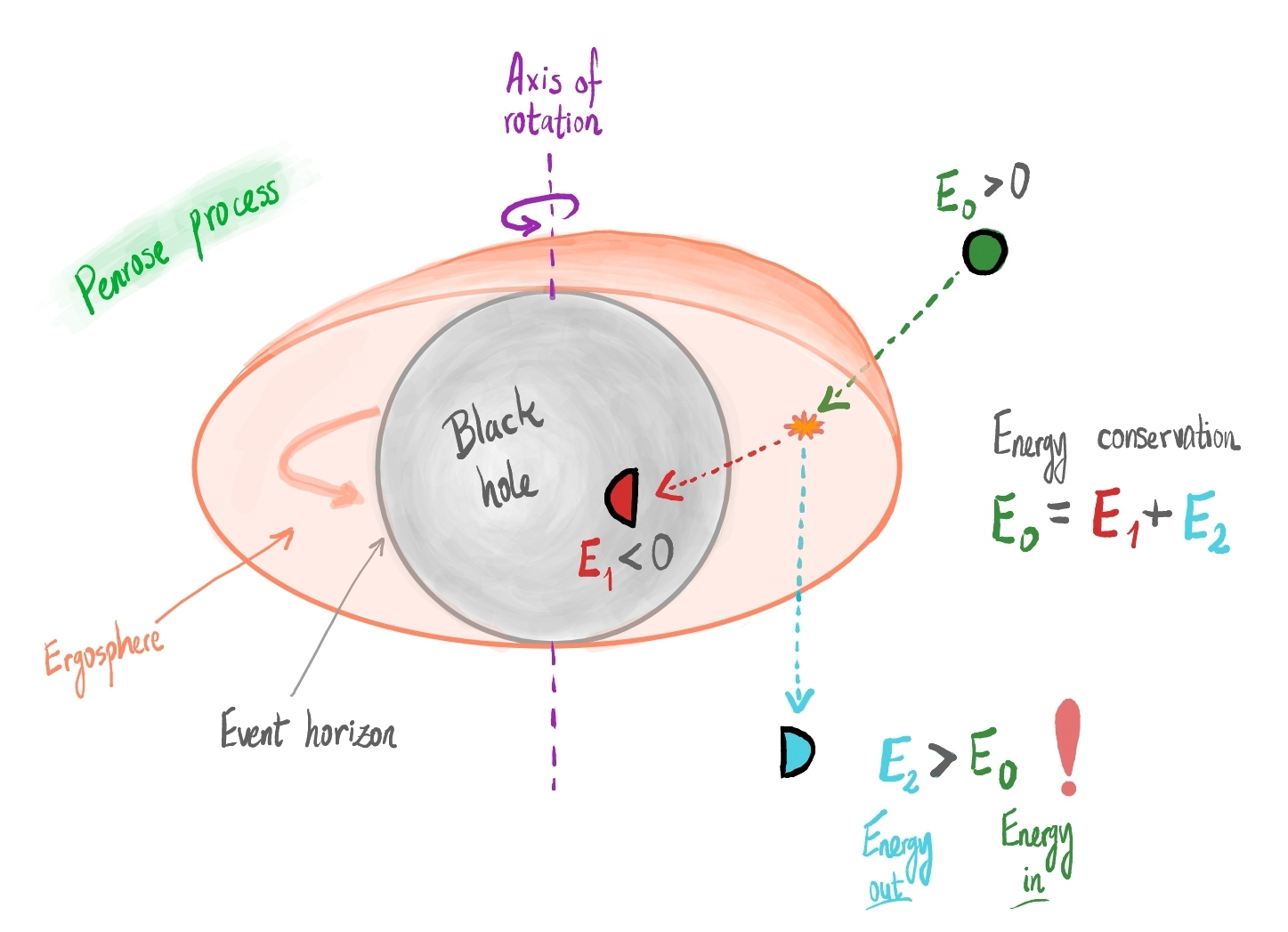
Figure 3: Cross-section diagram of a rotating black hole. The gray region marks the black hole lying beyond the event horizon. The oblate orange region surrounding it is the ergosphere. The axis of rotation is shown as a dashed purple line. The ergosphere meets the event horizon at the poles, where no rotation is felt. The Penrose process begins when an object (in green) is sent into the ergosphere. This object has positive energy E0>0, and splits inside the ergosphere into two fragments—the infalling one (in red) has negative energy E1<0, and the other one (in blue) escapes with an energy exceeding that of the original object (E2>E0).
In principle, this process can be repeated multiple times, extracting energy equivalent to up to about 29 percent (!) of the black hole’s mass [4] before reaching the theoretical limit at which the spin drops to zero and the ergosphere disappears. The more rapidly a black hole is spinning at the outset, the more energy can be extracted from it.
Perhaps distant alien civilizations are already using the Penrose mechanism to harvest clean energy from nearby spinning black holes? Who knows...
Illustrations: Noa Zilberman
Hebrew editing: Shir Rosenblum-Man
English editing: Gloria Volohonsky
References:
[1] A “Little, big science” post—a quick introduction to relativity and black holes
[2] “Little, big science” post on the 2020 Nobel Prize in Physics
[3] First appeared in Penrose’s 1969 paper Gravitational Collapse: The Role of General Relativity. A slightly longer (yet concise) description was published two years later in Nature.
Noa holds a PhD in Physics from the Technion and is currently a postdoctoral researcher at the Princeton Gravity Initiative at Princeton University. Her research focuses on quantum effects on black hole backgrounds. She also serves as a scientific editor at “Little, Big Science".
